32
- Giới thiệu
- Dữ liệu bỏ phiếu của Thượng viện và bài toán trực quan hóa
- Phép chiếu lên một đường thẳng
- Phép chiếu lên một mặt phẳng
- Phương có phương sai lớn nhất
- Phân tích phần tử chính quy
- PCA thưa
- Bài toán phương sai lớn nhất thưa
32.1 Giới thiệu
Trong nghiên cứu này, chúng ta lấy dữ liệu từ các cuộc bỏ phiếu về các dự luật tại Thượng viện Hoa Kỳ (2004-2006), và khám phá cách chúng ta có thể trực quan hóa dữ liệu bằng cách chiếu nó, đầu tiên lên một đường thẳng rồi đến một mặt phẳng. Chúng ta khảo sát cách có thể chọn đường thẳng hoặc mặt phẳng theo cách tối đa hóa phương sai trong kết quả, thông qua phương pháp phân tích thành phần chính. Cuối cùng, chúng ta xem xét một biến thể của PCA khuyến khích tính thưa của các phương chiếu cho phép hiểu được các dự luật nào chịu trách nhiệm chính cho phương sai trong dữ liệu.
Nguồn: VoteWorld.
32.2. Dữ liệu bỏ phiếu của Thượng viện và bài toán trực quan hóa
Dữ liệu
Dữ liệu bao gồm các lá phiếu của [latex]n=100[/latex] Thượng nghị sĩ tại Thượng viện Hoa Kỳ (2004-2006), cho tổng cộng [latex]m=542[/latex] dự luật. Các phiếu "Yay" ("Thuận") được biểu diễn bằng [latex]1[/latex], "Nay" ("Chống") bằng [latex]-1[/latex], và các phiếu khác được ghi là [latex]0[/latex]. (Một số sự phức tạp bị bỏ qua ở đây, chẳng hạn như khả năng ghép cặp các phiếu bầu.)
Dữ liệu này có thể được biểu diễn ở đây dưới dạng một ma trận "bỏ phiếu" [latex]m \times n[/latex] là [latex]X = [x_1,\ldots,x_n][/latex], với các phần tử được lấy từ [latex]\{-1,0,1\}[/latex]. Mỗi cột của ma trận bỏ phiếu [latex]x_j[/latex], [latex]j=1,\ldots,n[/latex] chứa các phiếu bầu của một Thượng nghị sĩ cho tất cả các dự luật; mỗi hàng chứa các phiếu bầu của tất cả các Thượng nghị sĩ về một dự luật cụ thể.
Ma trận bỏ phiếu Thượng viện: Các phiếu "Chống" màu đen, phiếu "Thuận" màu trắng, và các phiếu khác màu xám. Ma trận bỏ phiếu chuyển vị được hiển thị. Bức tranh có nhiều vùng xám, vì một số Thượng nghị sĩ được thay thế theo thời gian. Việc chỉ vẽ đồ thị ma trận dữ liệu thô thường không cung cấp nhiều thông tin.
Bài toán trực quan hoá
Ta có thể cố gắng trực quan hóa tập dữ liệu, bằng cách chiếu mỗi điểm dữ liệu (mỗi hàng hoặc cột của ma trận) lên (chẳng hạn) một không gian 1D, 2D hoặc 3D. Mỗi "cái nhìn" tương ứng với một phép chiếu cụ thể, tức là, một không gian con một, hai hoặc ba chiều mà ta chọn để chiếu dữ liệu lên. Bài toán trực quan hóa bao gồm việc chọn một phép chiếu thích hợp.
Có nhiều cách để phát biểu bài toán trực quan hóa, và không có cách nào vượt trội hơn các cách khác. Ở đây, chúng ta tập trung vào những điều cơ bản của bài toán đó.
32.3. Phép chiếu lên một đường thẳng
Để đơn giản hóa, trước hết chúng ta hãy xem xét bài toán đơn giản là biểu diễn tập dữ liệu nhiều chiều trên một đường thẳng, sử dụng phương pháp được mô tả tại đây.
Chấm điểm các Thượng nghị sĩ
Cụ thể, chúng ta muốn gán một số duy nhất, hay một "điểm số", cho mỗi cột của ma trận. Ta chọn một phương [latex]u[/latex] trong [latex]\mathbb{R}^m[/latex], và một vô hướng [latex]v[/latex] trong [latex]\mathbb{R}[/latex]. Điều này tương ứng với hàm "chấm điểm" afin [latex]f : \mathbb{R}^m \rightarrow \mathbb{R}[/latex], mà với một cột tổng quát [latex]x[/latex] trong [latex]\mathbb{R}^m[/latex] của ma trận dữ liệu, gán giá trị
[latex]\begin{align*} f(x) = u^T x + v. \end{align*}[/latex]
Do đó, ta thu được một véctơ các giá trị [latex]f[/latex] trong [latex]\mathbb{R}^n[/latex], với
[latex]\begin{align*} f_j = u^T x_j + v, \quad j=1,\ldots,n. \end{align*}[/latex]
Việc chỉnh tâm các giá trị này quanh số không thường hữu ích. Điều này có thể được thực hiện bằng cách chọn [latex]v[/latex] sao cho
[latex]\begin{align*} 0 &= \sum_{j=1}^n ( u^T x_j + v ) = u^T \left( \sum_{j=1}^n x_j \right) + n \cdot v, \end{align*}[/latex]
tức là: [latex]v = -u^T \hat{x},[/latex] trong đó
[latex]\begin{align*} \hat{x} := \frac{1}{n} \sum_{j=1}^n x_j \in \mathbb{R}^m \end{align*}[/latex]
là véctơ trung bình mẫu của các cột của ma trận (tức là, các điểm dữ liệu). Véctơ [latex]\hat{x}[/latex] có thể được diễn giải là "phản ứng trung bình" qua các thử nghiệm.
Các giá trị của hàm chấm điểm của chúng ta bây giờ có thể được biểu diễn là
[latex]\begin{align*} f(x) = u^T (x-\hat{x}). \end{align*}[/latex]
Để có thể so sánh giá trị tương đối của các phương khác nhau, ta có thể giả sử, mà không mất tính tổng quát, rằng véctơ [latex]u[/latex] được chuẩn hóa (sao cho [latex]|u|_2 = 1[/latex]).
Chỉnh tâm dữ liệu
Sẽ thuận tiện khi làm việc với ma trận dữ liệu "đã được chỉnh tâm", là
[latex]\begin{align*} X_{\text{cent}} = \left( \begin{array}{ccc} x_1 -\hat{x} & \ldots & x_n - \hat{x} \end{array}\right) = X - \hat{x}\mathbf{1}_n^T, \end{align*}[/latex]
trong đó [latex]\mathbf{1}_n[/latex] là véctơ gồm các số một trong [latex]\mathbb{R}^n[/latex].
Ta có thể tính toán véctơ (hàng) điểm số bằng cách sử dụng phép nhân ma trận-véctơ đơn giản:
[latex]\begin{align*} f = u^T X_{\text{cent}} \in \mathbb{R}^{1 \times m}. \end{align*}[/latex]
Ta có thể kiểm tra rằng trung bình của véctơ hàng trên bằng không:
[latex]\begin{align*} f\mathbf{1}_n = u^T X_{\text{cent}}\mathbf{1}_n = u^T(X - \hat{x}\mathbf{1}_n^T) \mathbf{1}_n = u^T(X\mathbf{1}_n - n \cdot \hat{x}) = 0. \end{align*}[/latex]
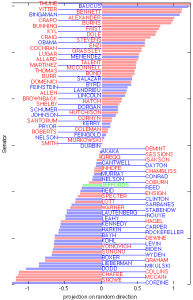
Ví dụ: trực quan hóa dọc theo một phương ngẫu nhiên
32.4. Phép chiếu lên một mặt phẳng
Ta cũng có thể thử chiếu dữ liệu lên một mặt phẳng, bao gồm việc gán hai điểm số cho mỗi điểm dữ liệu.
Ánh xạ chấm điểm
Điều này tương ứng với ánh xạ "chấm điểm" afin [latex]f : \mathbb{R}^m \rightarrow \mathbb{R}^2[/latex], mà với một cột tổng quát [latex]x[/latex] trong [latex]\mathbb{R}^m[/latex] của ma trận dữ liệu, gán giá trị hai chiều
\[ f(x) = \left( \begin{array}{c} u_1^Tx + v_1 \\ u_2^Tx+v_2 \end{array}\right) = U^Tx + v, \]
trong đó [latex]u_1,u_2 \in \mathbb{R}^m[/latex] là hai véctơ, và [latex]v_1,v_2[/latex] là hai vô hướng, trong khi [latex]U = [u_1,u_2] \in \mathbb{R}^{m \times 2}[/latex], [latex]v \in \mathbb{R}^2[/latex].
Ánh xạ afin [latex]f[/latex] cho phép tạo ra [latex]n[/latex] điểm dữ liệu hai chiều (thay vì [latex]m[/latex] chiều) [latex]f_j = U^Tx_j+v[/latex], [latex]j=1,\ldots,n[/latex]. Như trước đây, ta có thể yêu cầu các [latex]f_j[/latex] được chỉnh tâm:
\[0 = \sum_{j=1}^n f_j = \sum_{j=1}^n (U^Tx_j+v) ,\]
bằng cách chọn véctơ [latex]v[/latex] sao cho [latex]v = -U^T\hat{x}[/latex], trong đó [latex]\hat{x} \in \mathbb{R}^m[/latex] là "phản ứng trung bình" được định nghĩa ở trên. Ánh xạ chấm điểm (đã chỉnh tâm) của chúng ta có dạng
\[f(x) = U^T(x-\hat{x}).\]
Ta có thể gói gọn các điểm số trong ma trận [latex]2 \times n[/latex] là [latex]F=[f_1,\ldots,f_n][/latex]. Ma trận này có thể được biểu diễn dưới dạng phép nhân ma trận
\[F = U^TX_{\text{cent}} = \left( \begin{array}{c} u_1^TX_{\text{cent}} \\ u_2^TX_{\text{cent}} \end{array}\right),\]
với [latex]X_{\text{cent}}[/latex] là ma trận dữ liệu đã được chỉnh tâm được định nghĩa ở trên.
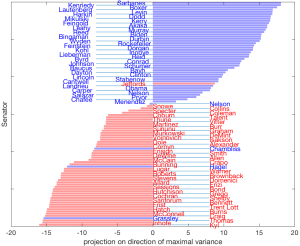
Rõ ràng, tùy thuộc vào mặt phẳng ta chọn để chiếu, ta sẽ nhận được những hình ảnh rất khác nhau. Một số mặt phẳng dường như "cung cấp nhiều thông tin" hơn những mặt phẳng khác. Chúng ta sẽ quay lại vấn đề này tại đây.
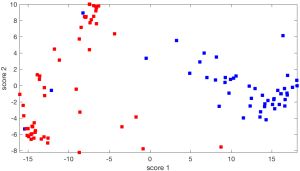 |
Phép chiếu hai chiều của ma trận bỏ phiếu Thượng viện: Phép chiếu cụ thể này dường như cho phép phân cụm các Thượng nghị sĩ theo đảng phái, và do đó cung cấp nhiều thông tin hơn. |
32.5. Phương có phương sai lớn nhất
Ta có thể thấy tại đây cách chọn một phương trong không gian dự luật, và sau đó chiếu ma trận dữ liệu bỏ phiếu Thượng viện lên phương đó, để trực quan hóa dữ liệu dọc theo một đường thẳng duy nhất. Rõ ràng, tùy thuộc vào cách ta chọn đường thẳng, ta sẽ nhận được những hình ảnh rất khác nhau. Một số cho thấy sự biến thiên lớn trong dữ liệu, những hình khác dường như có phạm vi hẹp hơn, ngay cả khi ta cẩn thận chuẩn hóa các phương.
Tiêu chí nào có thể là một tiêu chí tốt để chọn phương mà ta chiếu dữ liệu lên?
Có thể lập luận rằng một phương dẫn đến sự biến thiên lớn của dữ liệu được chiếu sẽ được ưu tiên hơn một phương có sự biến thiên nhỏ. Một phương có sự biến thiên cao "giải thích" dữ liệu tốt hơn, theo nghĩa là nó cho phép phân biệt giữa các điểm dữ liệu tốt hơn. Một tiêu chí mà ta có thể sử dụng để định lượng sự biến thiên trong một tập hợp các số thực là phương sai mẫu, là tổng bình phương của sự khác biệt giữa các số và giá trị trung bình của chúng.
Giải bài toán phương sai lớn nhất
Ta cần tìm một phương tối đa hóa phương sai thực nghiệm. Ta tìm một phương (đã được chuẩn hóa) [latex]u[/latex] sao cho phương sai thực nghiệm của các giá trị được chiếu [latex]u^Tx_j[/latex], [latex]j=1,\ldots,n[/latex], là lớn. Nếu [latex]\hat{x}[/latex] là véctơ trung bình của các [latex]x_j[/latex], thì giá trị trung bình của các giá trị được chiếu là [latex]u^T\hat{x}[/latex]. Do đó, phương có phương sai lớn nhất là phương giải bài toán tối ưu hóa
\[\max_{u : \|u\|_2 = 1} \frac{1}{n} \sum_{j=1}^n \left( (x_j-\hat{a})^Tu \right)^2.\]
Bài toán trên có thể được phát biểu lại như sau:
\[\max_{u : \|u\|_2 = 1} u^T\Sigma u,\]
trong đó
\[\Sigma := \frac{1}{n} \sum_{j=1}^n (x_j-\hat{a})(x_j-\hat{a})^T\]
là ma trận hiệp phương sai mẫu [latex]m \times m[/latex] của dữ liệu. Diễn giải của hệ số [latex]\Sigma_{kl}[/latex] là nó cung cấp hiệp phương sai giữa các phiếu bầu của Thượng nghị sĩ [latex]k[/latex] và Thượng nghị sĩ [latex]l[/latex].
Ta đã gặp bài toán trên trong phần trước, dưới tên gọi thương Rayleigh của một ma trận đối xứng. Việc giải bài toán chỉ đơn giản là tìm một véctơ riêng của ma trận hiệp phương sai [latex]\Sigma[/latex] tương ứng với giá trị riêng lớn nhất.
32.6. Phân tích phần tử chính quy
Ý tưởng chính
Ý tưởng chính đằng sau phân tích thành phần chính quy là trước hết tìm một phương tương ứng với phương sai lớn nhất giữa các điểm dữ liệu. Dữ liệu sau đó được chiếu lên siêu phẳng trực giao với phương đó. Ta thu được một tập dữ liệu mới, và tìm một phương mới có phương sai lớn nhất. Ta có thể dừng quá trình này khi đã thu thập đủ số phương (ví dụ, ba phương nếu ta muốn trực quan hóa dữ liệu trong không gian 3D).
Về mặt toán học, quá trình này tương đương với việc tìm phân tích giá trị riêng của một ma trận nửa xác định dương: ma trận hiệp phương sai của các điểm dữ liệu. Các phương có phương sai lớn tương ứng với các véctơ riêng có giá trị riêng lớn nhất của ma trận đó. Phép chiếu được sử dụng để thu được, chẳng hạn, một cái nhìn hai chiều với phương sai lớn nhất, có dạng [latex]x \rightarrow Px[/latex], trong đó [latex]P= [u_1,u_2]^T[/latex] là một ma trận chứa các véctơ riêng tương ứng với hai giá trị riêng đầu tiên.
Xấp xỉ hạng thấp
Trong một số trường hợp, ta không đặc biệt quan tâm đến việc trực quan hóa dữ liệu, mà chỉ đơn giản là xấp xỉ ma trận dữ liệu bằng một ma trận "đơn giản hơn".
Giả sử ta có một ma trận hiệp phương sai (mẫu) của dữ liệu, [latex]\Sigma[/latex]. Ta hãy tìm phân tích giá trị riêng của [latex]\Sigma[/latex]:
\[ \Sigma = \sum_{i=1}^m \lambda_i u_i u_i^T = U \textbf{diag}(\lambda_1,\ldots,\lambda_m) U^T, \]
trong đó [latex]U[/latex] là một ma trận trực giao [latex]m \times m[/latex]. Lưu ý rằng vết của ma trận đó có thể được diễn giải là tổng phương sai trong dữ liệu, là tổng của tất cả các phương sai của các phiếu bầu của mỗi Thượng nghị sĩ:
\[ \textbf{Trace} ( \Sigma ) = \sum_{i=1}^m \lambda_i. \]
Bây giờ ta hãy vẽ đồ thị các giá trị của [latex]\lambda_i[/latex] theo thứ tự giảm dần.
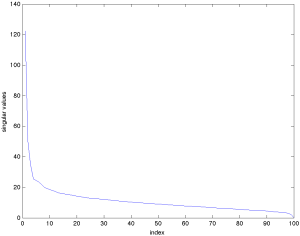 |
Hình ảnh này cho thấy các giá trị riêng của ma trận hiệp phương sai [latex]m \times m[/latex] của dữ liệu bỏ phiếu Thượng viện, vốn chứa hiệp phương sai giữa các phiếu bầu của mỗi cặp Thượng nghị sĩ. |
Rõ ràng, các giá trị riêng giảm rất nhanh. Có thể nói rằng "hầu hết thông tin" nằm trong giá trị riêng đầu tiên. Để làm cho lập luận này chặt chẽ hơn, ta có thể chỉ cần xem xét tỷ lệ:
\[\frac{\lambda_1}{\lambda_1 + \ldots + \lambda_m}\]
là tỷ lệ giữa phương sai của thành phần chính đầu tiên và tổng phương sai trong dữ liệu.
Trong trường hợp bỏ phiếu của Thượng viện, tỷ lệ này vào khoảng 90%. Thực tế, điều này đúng với hầu hết các mô hình bỏ phiếu trong các nền dân chủ trong lịch sử: giá trị riêng đầu tiên "giải thích hầu hết phương sai".
32.7. PCA thưa
Nhắc lại rằng phương có phương sai lớn nhất là một véctơ [latex]u \in \mathbb{R}^m[/latex] giải bài toán tối ưu hóa
\[ \max_{u : \|u\|_2 = 1} \frac{1}{n} \sum_{j=1}^n \left( (x_j-\hat{a})^Tu \right)^2 \Longleftrightarrow \max_{u : \|u\|_2 = 1} u^T\Sigma u, \; \; \text{ where } \Sigma := \frac{1}{n} \sum_{j=1}^n (x_j-\hat{a})(x_j-\hat{a})^T. \]
Ở đây [latex]\hat{x} := \frac{1}{n} \sum_{j=1}^n x_j[/latex] là tâm ước lượng. Ta thu được một tập dữ liệu mới bằng cách kết hợp các biến theo các phương được xác định bởi [latex]u[/latex]. Tập dữ liệu kết quả sẽ có cùng số chiều với tập dữ liệu ban đầu, nhưng mỗi chiều có một ý nghĩa khác nhau (vì chúng là các hình ảnh được chiếu tuyến tính của các biến ban đầu).
Như đã giải thích, ý tưởng chính đằng sau phân tích thành phần chính là tìm ra những phương tương ứng với phương sai lớn nhất giữa các điểm dữ liệu. Dữ liệu sau đó được chiếu lên siêu phẳng được căng bởi các thành phần chính này. Ta có thể dừng quá trình khi đã thu thập đủ số phương theo nghĩa là các phương mới giải thích phần lớn phương sai. Tức là, ta có thể chọn những phương tương ứng với điểm số cao nhất.
Ta cũng có thể tự hỏi liệu [latex]u[/latex] có thể chỉ có một vài tọa độ khác không hay không. Ví dụ, nếu phương tối ưu [latex]u[/latex] là [latex](0.01, 0.02, 200, 100) \in \mathbb{R}^4[/latex], thì rõ ràng là các dự luật thứ 3 và thứ 4 đặc trưng cho hầu hết các đặc điểm và ta có thể chỉ muốn loại bỏ các dự luật thứ 1 và thứ 2. Tức là, ta muốn điều chỉnh véctơ phương tối ưu thành [latex](0, 0, 200, 100) \in \mathbb{R}^4[/latex]. Sự điều chỉnh này tính đến tính thưa. Trong bối cảnh phân tích PCA, mỗi thành phần chính là các tổ hợp tuyến tính của tất cả các biến đầu vào. PCA thưa cho phép ta tìm các thành phần chính dưới dạng các tổ hợp tuyến tính chỉ chứa một vài biến đầu vào (do đó nó trông "thưa" trong không gian đầu vào). Tính năng này sẽ tăng cường khả năng diễn giải của tập dữ liệu kết quả và thực hiện giảm chiều trong không gian đầu vào. Việc giảm số lượng biến đầu vào sẽ hỗ trợ ta trong tập dữ liệu bỏ phiếu của thượng viện, vì có nhiều dự luật (biến đầu vào) hơn là thượng nghị sĩ (mẫu).
Chúng ta sẽ so sánh kết quả này của PCA với kết quả của PCA thưa dưới đây.
32.8 Bài toán phương sai lớn nhất thưa
Ý tưởng chính
Một sự tổng quát hóa toán học của PCA có thể thu được bằng cách sửa đổi bài toán tối ưu hóa PCA ở trên. Ta cố gắng tìm phương có phương sai lớn nhất là một véctơ [latex]u \in \mathbb{R}^m[/latex] giải bài toán tối ưu hóa
\[\begin{aligned}\max_{u : \|u\|_2 = 1, \|u\|_0 \leq k} \frac{1}{n} \sum_{j=1}^n \left( (x_j-\hat{a})^Tu \right)^2 \Longleftrightarrow \max_{u : \|u\|_2 = 1, \|u\|_0 \leq k} u^T\Sigma u,\end{aligned}\]
trong đó
\[\Sigma = \frac{1}{n} \sum_{j=1}^n (x_j-\hat{a})(x_j-\hat{a})^T.\]
Sự khác biệt là ta đặt thêm một ràng buộc [latex]\|u\|_0 \leq k[/latex], trong đó [latex]\|u\|_0[/latex] là số lượng tọa độ khác không trong véctơ [latex]u[/latex]. Ví dụ, [latex]\|(0.01, 0.02, 200, 100)\|_0 = 4[/latex] nhưng [latex]\|(0, 0, 200, 100)\|_0 = 2[/latex]. Ở đây, [latex]k[/latex] là một siêu tham số được xác định trước, mô tả độ thưa của không gian đầu vào mà ta muốn. Ràng buộc [latex]\|u\|_0 \leq k[/latex] này làm cho bài toán tối ưu hóa trở nên không lồi, và không có nghiệm dạng đóng giải tích. Nhưng ta vẫn có một nghiệm số và các tính chất thưa như đã giải thích. Tuy nhiên, [latex]\|u\|_0[/latex] làm cho bài toán tối ưu hóa không lồi và khó giải. Thay vào đó, ta thực hành một phương án nới lỏng chính quy hóa [latex]L_1[/latex]
\[\begin{aligned}\max_{u : \|u\|_2 = 1} \frac{1}{n} \sum_{j=1}^n \left( (x_j-\hat{a})^Tu \right)^2 + \lambda \|u\|_1 \Longleftrightarrow \max_{u : \|u\|_2 = 1} u^T\Sigma u + \lambda \|u\|_1.\end{aligned}\]
Bài toán tối ưu hóa này là lồi và có thể được giải bằng phương pháp số; đây là cái gọi là phương pháp PCA thưa (SPCA). Tham số [latex]\lambda[/latex] là một siêu tham số được xác định trước mà ta giới thiệu như một tham số phạt, có thể được điều chỉnh, như ta sẽ thấy dưới đây.
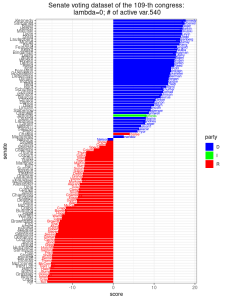
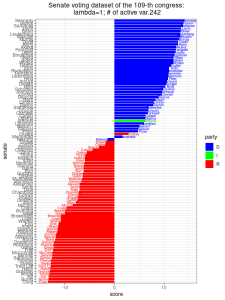
Phân tích bộ dữ liệu bầu cử Thượng viện
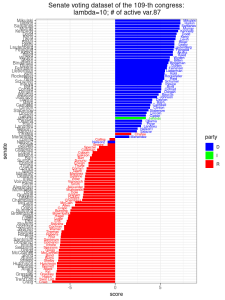
Ta có thể áp dụng phương pháp SPCA vào tập dữ liệu bỏ phiếu của Thượng viện, với [latex]\lambda = 0[/latex] (tức là PCA) và tăng [latex]\lambda[/latex] lên các giá trị 1, 10, và 1000. Trong mỗi thiết lập, ta cũng ghi lại số lượng tọa độ khác không của [latex]u_{\text{max}}[/latex], là một nghiệm của bài toán tối ưu hóa SPCA ở trên. Vì mỗi tọa độ của [latex]u_{\text{max}}[/latex] biểu thị kết quả bỏ phiếu của một dự luật, ta gọi số lượng tọa độ khác không của [latex]u_{\text{max}}[/latex] là số lượng biến hoạt động. Từ các kết quả dưới đây, ta không quan sát thấy nhiều thay đổi trong sự phân chia các đảng phái được cho bởi các thành phần chính. Khi [latex]\lambda[/latex] tăng lên 1000, chỉ còn lại 7 biến hoạt động. 7 dự luật tương ứng, vốn quan trọng để phân biệt các đảng phái của các thượng nghị sĩ, là:
- Vấn đề năng lượng (8 Energy Issues LIHEAP Funding Amendment 3808)
- Vấn đề phá thai (16 Abortion Issues Unintended Pregnancy Amendment 3489)
- Ngân sách, Chi tiêu và Thuế (34 Budget, Spending and Taxes Hurricane Victims Tax Benefit Amendment 3706)
- Ngân sách, Chi tiêu và Thuế (36 Budget, Spending and Taxes Native American Funding Amendment 3498)
- Vấn đề năng lượng( 47 Energy Issues Reduction in Dependence on Foreign Oil 3553)
- Vấn đề Quân sự (59 Military Issues Habeas Review Amendment 3908)
- Kinh doanh và tiêu dùng (81 Business and Consumers Targeted Case Management Amendment 3664)