• Hồi quy tuyến tính thông qua bình phương tối thiểu.
• Các mô hình tự hồi quy (AR) để dự báo chuỗi thời gian.

[latexpage]

26.1. Hồi quy tuyến tính thông qua bình phương tối thiểu

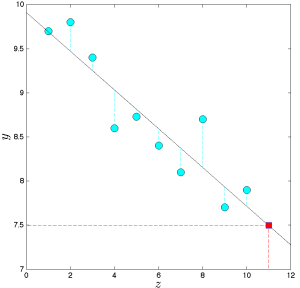
Hồi quy tuyến tính dựa trên ý tưởng khớp một hàm tuyến tính qua các điểm dữ liệu.

Ở dạng cơ bản, bài toán được phát biểu như sau. Ta được cho các dữ liệu $(y_i, x_i), i=1, \ldots, m$ trong đó $x_i \in \mathbb{R}^n$ là “đầu vào” và $y_i \in \mathbb{R}$ là “đầu ra” cho phép đo thứ $i$. Ta tìm một hàm tuyến tính $f: \mathbb{R}^n \to \mathbb{R}$ sao cho các giá trị $f(x_i)$ gần với các giá trị $y_i$ tương ứng.

Trong \textit{hồi quy bình phương tối thiểu}, cách ta đánh giá một hàm ứng viên $f$ khớp với dữ liệu tốt đến đâu là thông qua chuẩn Euclid (bình phương):

$$
\sum_{i=1}^m\left(y_i-f\left(x_i\right)\right)^2 .
$$

Vì một hàm tuyến tính $f$ có dạng $f(x)=\theta^T x$ với một véctơ $\theta \in \mathbb{R}^n$ nào đó, bài toán tối thiểu hóa tiêu chuẩn trên có dạng

$$
\min _\theta \sum_{i=1}^m\left(y_i-x_i^T \theta\right)^2 .
$$

Ta có thể phát biểu bài toán này dưới dạng một bài toán bình phương tối thiểu:

$$
\min _\theta\|A \theta-y\|_2,
$$

trong đó

$$
A=\left(\begin{array}{c}
x_1^T \\
\vdots \\
x_m^T
\end{array}\right)
$$

Phương pháp hồi quy tuyến tính có thể được mở rộng cho nhiều chiều, tức là cho các bài toán mà đầu ra trong bài toán trên có nhiều hơn một chiều (xem tại đây). Nó cũng có thể được mở rộng cho bài toán khớp các đường cong phi tuyến.

	Trong ví dụ này, ta tìm cách phân tích phản ứng của khách hàng đối với việc tăng giá của một mặt hàng nhất định. Ta được cho các điểm dữ liệu hai chiều $\left(x_i, y_i\right), i=1, \ldots, m$. Các giá trị $x_i$ chứa giá của mặt hàng, và các giá trị $y_i$ là số lượng khách hàng trung bình mua mặt hàng ở mức giá đó.
	Phương trình tổng quát của một đường thẳng không thẳng đứng là $y=\theta_1 x+\theta_2$, trong đó $\theta=\left(\theta_1, \theta_2\right)$ chứa các biến quyết định. Chất lượng của việc khớp một đường thẳng tổng quát được đo bằng tổng bình phương sai số ở thành phần $y$ (các đường chấm màu xanh). Do đó, sự khớp bình phương tối thiểu tốt nhất được thu được thông qua bài toán bình phương tối thiểu
	$$ \min _\theta \sum_{i=1}^m\left(\theta_1 x_i+\theta_2-y_i\right)^2 . $$
	Một khi đường thẳng được xác định, ta có thể được sử dụng để dự báo giá trị của số lượng khách hàng trung bình mua mặt hàng ($y$) cho một mức giá mới ($x$). Dự báo được thể hiện bằng màu đỏ.

Xem thêm:

• Bài toán Gauss.

26.2. Các mô hình tự hồi quy (AR) để dự báo chuỗi thời gian

trong đó $\theta_i$ là các hệ số hằng và $m$ là “độ dài bộ nhớ” của mô hình. Diễn giải của mô hình là đầu ra tiếp theo là một hàm tuyến tính của các giá trị trong quá khứ. Các biến thể phức tạp của mô hình tự hồi quy được sử dụng rộng rãi để dự báo các chuỗi thời gian phát sinh trong tài chính và kinh tế.

Để tìm véctơ hệ số $\theta=(\theta_1, \ldots, \theta_m)$ trong $\mathbb{R}^m$, ta thu thập các quan sát $\left(y_t\right)_{0 \leq t \leq T}$ (với $T \geq m$) của chuỗi thời gian, và cố gắng tối thiểu hóa tổng bình phương sai số trong phương trình trên:

\[ \min _\theta: \sum_{t=m}^T\left(y_t-\theta_1 y_{t-1}-\ldots-\theta_m y_{t-m}\right)^2.\]

Bài toán này có thể được biểu diễn như một bài toán bình phương tối thiểu tuyến tính, với dữ liệu $A, y$ thích hợp.