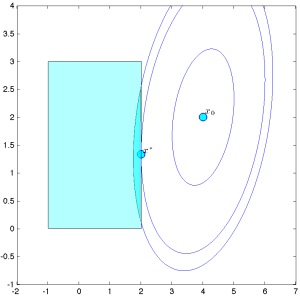
Như một ví dụ đồ chơi về một bài toán tối ưu hóa hai biến, xét bài toán
\[ \min _x 0.9 x_1^2-0.4 x_1 x_2-0.6 x_2^2-6.4 x_1-0.8 x_2: -1 \leq x_1 \leq 2, \quad 0 \leq x_2 \leq 3. \]
(Lưu ý rằng cụm từ "với điều kiện" đã được thay thế bằng ký hiệu dấu hai chấm.)
Bài toán có thể được đưa về dạng chuẩn
\[ p^*:=\min _x f_0(x): f_i(x) \leq 0, \quad i=1, \ldots, m, \]
trong đó:
● Biến quyết định là [latex]\left(x_1, x_2\right) \in \mathbb{R}^2[/latex];
● Hàm mục tiêu [latex]f_0: \mathbb{R}^2 \rightarrow \mathbb{R}[/latex], nhận các giá trị
[latex]f_0(x):=0.9 x_1^2-0.4 x_1 x_2-0.6 x_2^2-6.4 x_1-0.8 x_2;[/latex]
● Các hàm ràng buộc [latex]f_i: \mathbb{R}^2 \rightarrow \mathbb{R}, i=1,2,3,4[/latex] nhận các giá trị
\[ \begin{aligned} & f_1(x):=-x_1-1, \\ & f_2(x):=x_1-2, \\ & f_3(x):=-x_2, \\ & f_4(x):=x_2-3. \end{aligned} \]
● [latex]p^*[/latex] là giá trị tối ưu, là [latex]p^*=-10.2667[/latex].
● Tập tối ưu là tập đơn tử [latex]\mathbf{X}^{\text {opt }}=\left\{x^*\right\}[/latex], với
\[ x^*=\left(\begin{array}{c} 2.00 \\ 1.33 \end{array}\right). \]
Vì tập tối ưu không rỗng, bài toán là khả thi.
Ta có thể biểu diễn bài toán ở dạng epigraph, như sau
\[ \min _{x, t} t: t \geq 0.9 x_1^2-0.4 x_1 x_2-0.6 x_2^2-6.4 x_1-0.8 x_2, \quad -1 \leq x_1 \leq 2, \quad 0 \leq x_2 \leq 3. \]