7.1. Dữ liệu bỏ phiếu của Thượng viện

Trong phần này, chúng ta tập trung vào một tập dữ liệu chứa các phiếu bầu của các Thượng nghị sĩ Hoa Kỳ. Tập dữ liệu này có thể được biểu diễn dưới dạng một tập hợp [latex]n = 100[/latex] vectơ [latex]x_j[/latex], [latex]j = 1, \cdots, n[/latex] trong [latex]\mathbb{R}^m[/latex], với [latex]m=645[/latex] là số lượng dự luật và [latex]n=100[/latex] là số lượng Thượng nghị sĩ. Do đó, [latex]x_j[/latex] chứa tất cả các phiếu bầu của Thượng nghị sĩ [latex]j[/latex] và thành phần thứ [latex]i[/latex] của [latex]x_j[/latex] chứa phiếu bầu của Thượng nghị sĩ đó đối với dự luật [latex]i[/latex].

Ma trận bỏ phiếu của Thượng viện: Hình ảnh này cho thấy các phiếu bầu của [latex]n=100[/latex] Thượng nghị sĩ trong Thượng viện Hoa Kỳ giai đoạn 2004-2006, tổng cộng là [latex]m=645[/latex] dự luật. Các phiếu bầu “Có” được biểu thị bằng [latex]1[/latex], “Không” bằng [latex]-1[/latex] và các phiếu bầu khác được ghi lại là [latex]0[/latex]. Mỗi hàng biểu thị các phiếu bầu của một Thượng nghị sĩ duy nhất và mỗi cột chứa các phiếu bầu của tất cả các Thượng nghị sĩ cho một dự luật cụ thể. Các vectơ [latex]x_j[/latex], [latex]j=1, \cdots, m =645[/latex] có thể được đọc dưới dạng các hàng trong hình.

7.2. Trực quan hóa dữ liệu chiều cao bằng phép chiếu

Như đã thấy trong hình trên, việc chỉ vẽ đồ thị dữ liệu thô thường không cung cấp nhiều thông tin.
Chúng ta có thể cố gắng trực quan hóa tập dữ liệu bằng cách chiếu mỗi điểm dữ liệu (mỗi hàng hoặc cột của ma trận) lên (ví dụ) một không gian một, hai hoặc ba chiều. Mỗi “khung nhìn” tương ứng với một phép chiếu cụ thể, tức là một không gian con một, hai hoặc ba chiều cụ thể mà chúng ta chọn để chiếu dữ liệu lên. Chúng ta hãy chi tiết ý nghĩa của việc chiếu trên một tập hợp một chiều, tức là trên một đường thẳng.

Việc chiếu trên một đường thẳng cho phép gán một số duy nhất hoặc “điểm số” cho mỗi điểm dữ liệu thông qua một tích vô hướng. Chúng ta chọn một hướng (chuẩn hóa) [latex]u \in \mathbb{R}^m[/latex] và một đại lượng vô hướng [latex]v \in \mathbb{R}[/latex]. Điều này tương ứng với hàm “chấm điểm” affine [latex]f: \mathbb{R}^m \rightarrow \mathbb{R}[/latex], mà với một điểm dữ liệu tổng quát [latex]x \in \mathbb{R}^m[/latex], gán giá trị:
[latex]\begin{align*}f(x) = u^Tx+v\end{align*}[/latex]

Do đó, chúng ta thu được một vectơ các giá trị [latex]f \in \mathbb{R}^n[/latex], với các thành phần [latex]f_j = u^Tx_j + v[/latex], [latex]j = 1, \cdots, n[/latex]. Thông thường, việc căn chỉnh các điểm số này xung quanh số 0 là hữu ích. Điều này có thể được thực hiện bằng cách chọn v sao cho:
[latex]\begin{align*}0 = \sum\limits_{j=1}^{n} (u^Tx_j + v) = u^T \left(\sum\limits_{j=1}^{n} x_j \right) +n\cdot v\end{align*}[/latex]

Điều kiện trung bình bằng không ngụ ý [latex]v = u^T \widehat{x}[/latex], trong đó:
[latex]\begin{align*}\widehat{x}:=\frac{1}{n} \sum\limits_{j=1}^{n} x_j \in \mathbb{R}^m\end{align*}[/latex]
là vectơ của các giá trị trung bình mẫu của các điểm dữ liệu khác nhau.

Vectơ [latex]\widehat{x}[/latex] có thể được hiểu là “phản hồi trung bình” trên các điểm dữ liệu (phiếu bầu trung bình trên các Thượng nghị sĩ trong ví dụ đang xét). Các giá trị của hàm chấm điểm của chúng ta bây giờ có thể được biểu diễn như sau:
[latex]\begin{align*}f(x) = u^T(x-\widehat{x})\end{align*}[/latex]

Để có thể so sánh ưu điểm tương đối của các hướng khác nhau, chúng ta có thể giả định, mà không mất tính tổng quát, rằng vectơ hướng u đã được chuẩn hóa (để [latex]||u||_2=1[/latex]).

Lưu ý rằng định nghĩa [latex]f(x)[/latex] ở trên của chúng ta phù hợp với ý tưởng chiếu các điểm dữ liệu [latex]x_i - \widehat{x}[/latex] trên đường thẳng đi qua gốc tọa độ và có hướng chuẩn hóa [latex]u[/latex]. Thật vậy, thành phần của [latex]x_i - \widehat{x}[/latex] trên đường thẳng là [latex]u^T(x_i - \widehat{x})[/latex].

Trong ví dụ về bỏ phiếu của Thượng viện ở trên, một phép chiếu cụ thể (tức là một hướng trong [latex]\mathbb{R}^m[/latex]) tương ứng với việc gán một “điểm số” cho mỗi Thượng nghị sĩ, và do đó biểu diễn tất cả các Thượng nghị sĩ dưới dạng một giá trị duy nhất trên một đường thẳng. Chúng ta sẽ chiếu dữ liệu theo một vectơ trong không gian “dự luật”, là [latex]\mathbb{R}^m[/latex]. Tức là, chúng ta sẽ tạo các tổ hợp tuyến tính của các dự luật, sao cho [latex]m=642[/latex] phiếu bầu của mỗi Thượng nghị sĩ được giảm thành một số duy nhất, hay “điểm số”. Vì chúng ta đã căn chỉnh dữ liệu của mình, điểm số trung bình (trên các Thượng nghị sĩ) bằng không.

7.3. Ví dụ

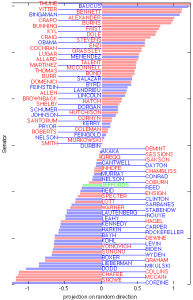
Phép chiếu theo một hướng ngẫu nhiên

Điểm số thu được với hướng ngẫu nhiên: Hình ảnh này cho thấy các giá trị của phép chiếu các phiếu bầu của Thượng nghị sĩ [latex]x_j - \widehat{x}[/latex] (tức là đã loại bỏ giá trị trung bình trên các Thượng nghị sĩ) trên một hướng “dự luật ngẫu nhiên” (đã chuẩn hóa). Mỗi điểm số là một số được cho bởi [latex]u_{rand}^T(x_j - \widehat{x})[/latex], với [latex]u_{rand}[/latex] là một vectơ ngẫu nhiên (được chuẩn hóa để có chuẩn Euclid bằng 1). Chúng ta hiển thị sự liên kết đảng phái, với màu xanh lá cây tương ứng với Thượng nghị sĩ độc lập Jeffords. Phép chiếu này không cho thấy cấu trúc rõ ràng; đặc biệt, nó không tiết lộ liên kết đảng phái.

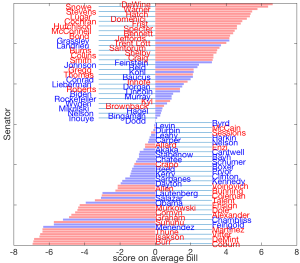
Phép chiếu theo vectơ “toàn 1”

Rõ ràng, không phải tất cả các hướng đều “tốt”, theo nghĩa tạo ra các đồ thị giàu thông tin. Ở đây, chúng ta thảo luận về một nguyên tắc chung cho phép chọn một hướng “giàu thông tin”. Nhưng đối với tập dữ liệu này, một phỏng đoán tốt có thể là chọn hướng tương ứng với “dự luật trung bình”. Tức là, chúng ta chọn hướng [latex]u[/latex] song song với vectơ toàn một trong [latex]\mathbb{R}^m[/latex], được chia tỷ lệ thích hợp để chuẩn Euclid của nó bằng một.

	Điểm số thu được với hướng toàn 1: Hình ảnh này cho thấy các giá trị của phép chiếu các phiếu bầu của Thượng nghị sĩ [latex]x_j - \widehat{x}[/latex] (tức là đã loại bỏ giá trị trung bình trên các Thượng nghị sĩ) trên một hướng “dự luật trung bình” (đã chuẩn hóa). Mỗi điểm số là một số được cho bởi [latex]u_{avg}^T(x_j - \widehat{x})[/latex], với [latex]u_{avg}[/latex] là một vectơ có các phần tử đều bằng [latex]1/\sqrt{m}[/latex] (nó được chuẩn hóa để có chuẩn Euclid bằng 1). Phép chiếu này cho thấy rõ sự liên kết đảng phái của mỗi Thượng nghị sĩ, mặc dù thông tin này không được cung cấp cho thuật toán chiếu. Giải thích là hành vi của các Thượng nghị sĩ đối với một “dự luật trung bình” gần như xác định đầy đủ sự liên kết đảng phái của người đó. Lưu ý phạm vi của đồ thị (khoảng [latex][-6;6][/latex]), cao hơn so với vectơ ngẫu nhiên (khoảng [latex][-1;1][/latex]), cho phép phân tán điểm số tốt hơn.