Một hàm tuyến tính bình phương là một hàm bậc hai [latex]q: \mathbb{R}^n \rightarrow \mathbb{R}[/latex] có dạng
[latex]\begin{align*} q(x) &= (v^Tx)^2, \end{align*}[/latex]
với một véctơ nào đó [latex]v \in \mathbb{R}^n[/latex].
Hàm số triệt tiêu trên không gian trực giao với [latex]v[/latex], đây là siêu phẳng được định nghĩa bởi một phương trình tuyến tính duy nhất [latex]v^Tx = 0[/latex]. Do đó, thực chất hàm này là một chiều: nó chỉ thay đổi theo phương của [latex]v[/latex].
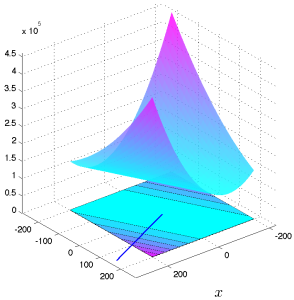 |
Tập mức và đồ thị của một hàm bậc hai dyadic, tương ứng với véctơ [latex]v= (2,1)[/latex]. Hàm số không đổi dọc theo các siêu phẳng trực giao với [latex]v[/latex]. |

