Một ma trận đối xứng là một cách để mô tả một đồ thị vô hướng có trọng số: mỗi cạnh trong đồ thị được gán một trọng số [latex]W_{ij}[/latex]. Vì đồ thị là vô hướng, trọng số của cạnh không phụ thuộc vào hướng (từ [latex]i[/latex] đến [latex]j[/latex] hay ngược lại). Do đó, [latex]W[/latex] là ma trận đối xứng.
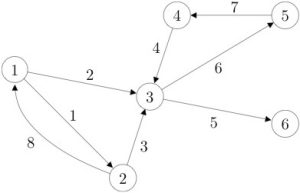 |
Với đồ thị trong hình, ta có thể liên kết nó với đồ thị vô hướng tương ứng, thu được bằng cách bỏ qua hướng của các mũi tên. Giả sử rằng tất cả các cạnh có cùng trọng số, đồ thị vô hướng có ma trận trọng số cạnh được cho bởi
[latex]W=\left[\begin{array}{cccccccc} 1 & 1 & 0 & 0 & 0 & 0 & 0 & -1 \\ -1 & 0 & 1 & 0 & 0 & 0 & 0 & 1 \\ 0 & -1 & -1 & -1 & 1 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & 0 & 0 & -1 & 1 & 0 \\ 0 & 0 & 0 & 0 & -1 & 0 & 0 & 0 \end{array}\right][/latex]
|
|
Xem thêm:


