2.8 First Derivative and the Extrema
2.8 First Derivative and the Extrema
In theory and applications, we often want to maximize or minimize some quantity. An engineer may want to maximize the speed of a new computer or minimize the heat produced by an appliance. A manufacturer may want to maximize profits and market share or minimize waste.
A student may want to maximize a grade in calculus or minimize the hours of study needed to earn a particular grade.
Without calculus, we only know how to find the optimum points in a few specific examples (for example, we know how to find the vertex of a parabola). But what if we need to optimize an unfamiliar function?
The best way we have without calculus is to examine the graph of the function, perhaps using technology. But our view depends on the viewing window we choose – we might miss something important. In addition, we’ll probably only get an approximation this way. (In some cases, that will be good enough.)
Calculus provides ways of drastically narrowing the number of points we need to examine to find the exact locations of maximums and minimums, while at the same time ensuring that we haven’t missed anything important.
Video Demonstration
Optimization/finding extrema
© 2014 Eric Bancroft
Maxima and Minima
Before we examine how calculus can help us find maximums and minimums, we need to define the concepts we will develop and use.
Definitions (Local Maxima and Minima)
[latex]f(x)[/latex] has a local maximum at [latex]x=a[/latex] if [latex]f(a) \geq f(x)[/latex] for all [latex]x[/latex] near [latex]a[/latex].
[latex]f(x)[/latex] has a local minimum at [latex]x=a[/latex] if [latex]f(a) \leq f(x)[/latex] for all [latex]x[/latex] near [latex]a[/latex].
[latex]f(x)[/latex] has a local extreme at [latex]x=a[/latex] if [latex]f(a)[/latex] is a local maximum or minimum.
The plurals of these are maxima and minima. We often simply say “max” or “min;” it saves a lot of syllables. Some books say “relative” instead of “local.”
The process of finding maxima or minima is called optimization.
Definitions (Global Maxima and Minima)
[latex]f(x)[/latex] has a global maximum at [latex]x=a[/latex] if [latex]f(a) \geq f(x)[/latex] for all [latex]x[/latex] in the domain of [latex]f(x).[/latex]
[latex]f(x)[/latex] has a global minimum at [latex]x=a[/latex] if [latex]f(a) \leq f(x)[/latex] for all [latex]x[/latex] in the domain of [latex]f(x)[/latex].
[latex]f(x)[/latex] has a global extreme at [latex]x=a[/latex] if [latex]f(a)[/latex] is a global maximum or minimum. Some books say “absolute” instead of “global.”
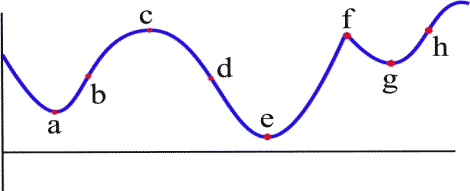
The local and global extremes of the function in Figure 1 are labeled. You should notice that every global extreme is also a local extreme, but there are local extremes that are not global extremes.
If [latex]h(x)[/latex] is the height of the earth above sea level at the location [latex]x[/latex], then the global maximum of [latex]h[/latex] is [latex]h[/latex](summit of Mt. Everest) = 29,028 feet. The local maximum of [latex]h[/latex] for the United States is [latex]h[/latex](summit of Mt. McKinley) = 20,320 feet. The local minimum of [latex]h[/latex] for the United States is [latex]h[/latex](Death Valley) = -282 feet.
Example 1
The table shows the annual calculus enrollments at a large university. Which years had local maximum or minimum calculus enrollments? What were the global maximum and minimum enrollments in calculus?
| Year | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 |
| Enrollment | 1257 | 1324 | 1378 | 1336 | 1389 | 1450 | 1523 | 1582 | 1567 | 1545 | 1571 |
Answer:
There were local maxima in 2002 and 2007; the global maximum was 1582 students in 2007.
There were local minima in 2003 and 2009; the global minimum was 1257 students in 2000.
We choose not to think of 2000 as a local minimum or 2010 as a local maximum; however, some books would include the endpoints. We are allowed to have a global maximum or global minimum at an endpoint.
Video Demonstration
Example 1
© 2014 Eric Bancroft
Finding maxima and minima of a function
What must the tangent line look like at a local max or min? Look at these two graphs again you’ll see that at all the extreme points, the tangent line is horizontal (so [latex]f' = 0[/latex]). There is one cusp in the blue graph – the tangent line is vertical there (so [latex]f'[/latex] is undefined).
That gives us the clue how to find extreme values.
Definition of a critical number
A critical number for a function [latex]f[/latex] is a value [latex]x = a[/latex] in the domain of [latex]f[/latex] where either [latex]f'(a) = 0[/latex] or [latex]f'(a)[/latex] is undefined.
A critical point for a function [latex]f[/latex] is a point [latex](a, f(a))[/latex] where [latex]a[/latex] is a critical number of [latex]f[/latex].
A local maximum or minimum of [latex]f[/latex] can only occur at a critical point but not every critical point is a point of a minimum or a maximum.
Example 2
Find the critical points of [latex]f(x) = x^3 - 6x^2 + 9x + 2[/latex].
Answer: critical points? [latex]\to[/latex] points [latex](c,f(c))[/latex] where [latex]c[/latex] is a critical number
Therefore we need to identify the critical numbers.
A critical number of [latex]f[/latex] can occur only for values of [latex]x[/latex] in the domain of the function where [latex]f'(x) = 0[/latex] or where [latex]f'[/latex] does not exist.
Since [latex]f(x)[/latex] is a polynomial, its domain is all real numbers.
[latex]f '(x) = 3x^2 - 12x + 9 = 3(x^2 - 4x + 3) = 3(x - 1)(x - 3)[/latex]
Since [latex]f'(x)[/latex] is a polynomial, it is never undefined.
We have that [latex]f'(x) = 0[/latex] at [latex]x = 1[/latex] and [latex]x = 3[/latex] (and no other values of [latex] x[/latex]). Both of these values are in the domain of [latex]f(x)[/latex].
Therefore, the critical numbers are [latex]x = 1[/latex] and [latex]x= 3[/latex]. Since [latex]f(1)=6[/latex] and [latex]f(3)=2[/latex], the critical points are [latex](1, 6)[/latex] and [latex](3, 2)[/latex].
These are the only possible locations of local extremes of [latex]f[/latex]. We haven’t discussed yet how to tell whether either of these points is actually a local extreme of [latex]f[/latex], or which kind it might be. But we can be certain that no other point is a local extreme.
The graph of [latex]f[/latex] below shows that [latex](1, f(1) ) = (1, 6)[/latex] is a local maximum and [latex](3, f(3) ) = (3, 2)[/latex] is a local minimum. This function does not have a global maximum or minimum.
Example 3
Find all local extrema of [latex]f(x) = x^3[/latex].
Answer: local extrema of [latex]f[/latex]?
Local extrema occur at critical numbers, so we need to identify the critical numbers, i.e., alues of [latex]x[/latex] in the domain of the function where [latex]f'(x) = 0[/latex] or where [latex]f'[/latex] does not exist.
Since [latex]f(x)[/latex] is a polynomial, its domain is all real numbers.
Since [latex]f'(x) = 3x^2[/latex], [latex]f(x)[/latex] is differentiable for all [latex]x[/latex] and so [latex]f'(x)[/latex] is never undefined.
On the other hand, the only place where [latex]f'(x) = 0[/latex] is at [latex]x = 0[/latex], which is in the domain of the function, so the only candidate for an extrema is the critical number [latex]x=0[/latex].
If [latex]x \gt 0[/latex] then [latex]f(x) = x^3 \gt 0 = f(0)[/latex], so [latex]f(0)[/latex] is not a local maximum.
Similarly, if [latex]x \lt 0[/latex] then [latex]f(x) = x^3 \lt 0 = f(0)[/latex] so [latex]f(0)[/latex] is not a local minimum.
Since [latex]x=0[/latex] was the only potential candidate, the function [latex]f(x) = x^3[/latex] does not have any local extrema.
Looking at the graph of the function below, we can see why [latex]x=0[/latex] appeared to be a potential candidate but is not a location of the extrema.
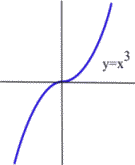
Remember this example! It is not enough to find the critical points – we can only say that [latex]f[/latex] might have a local extreme at the critical points.
First and Second Derivative Tests
Is that critical point a Maximum or Minimum (or Neither)?
Once we have found the critical points of [latex]f[/latex], we still have the problem of determining whether these points are maxima, minima or neither.
All of the graphs in the figure below have a critical point at [latex](2, 3)[/latex]. It is clear from the graphs that the point (2,3) is a local maximum in (a) and (d), (2,3) is a local minimum in (b) and (e), and (2,3) is not a local extreme in (c) and (f).
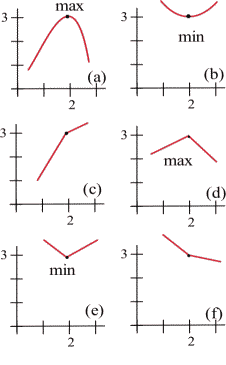
The critical numbers only give the possible locations of extremes, and some critical numbers are not the locations of extremes. The critical numbers are the candidates for the locations of maxima and minima.
Derivative of a function and extrema of the function
Four possible shapes of graphs are shown here – in each graph, the point marked by an arrow is a critical point, where [latex]f'(x) = 0[/latex]. What happens to the derivative near the critical point?
At a local max, such as in the graph on the left, the function increases on the left of the local max, then decreases on the right. The derivative is first positive, then negative at a local max. At a local min, the function decreases to the left and increases to the right, so the derivative is first negative, then positive. When there isn’t a local extreme, the function continues to increase (or decrease) right past the critical point – the derivative doesn’t change sign.
The First Derivative Test for Extrema
- If [latex]f'(x)[/latex] changes from positive to negative at [latex]x = c[/latex], then [latex]f[/latex] has a local maximum at [latex](c, f(c))[/latex].
- If [latex]f'(x)[/latex] changes from negative to positive at [latex]x = c[/latex], then [latex]f[/latex] has a local minimum at [latex](c, f(c))[/latex].
- If [latex]f'(x)[/latex] does not change sign at [latex]x = c[/latex], then [latex](c, f(c))[/latex] is neither a local maximum nor a local minimum.
Video Demonstration
Finding local extema: Example A
© 2014 Eric Bancroft
Example 4
Find the critical points of [latex]f(x) = x^3 - 6x^2 + 9x + 2[/latex] and classify them as local max, local min, or neither.
Answer: critical points? extrema at critical points?
Domain: [latex]f[/latex] is a polynomial so the domain is all real numbers.
We already found the critical points in Example 3. They are [latex](1, 6)[/latex]and [latex](3, 2).[/latex]
Now we can use the first derivative test to classify each. Recall that [latex]f'(x) = 3x^2 - 12x + 9 = 3(x^2 - 4x + 3) = 3(x - 1)(x - 3)[/latex]. The factored form is easiest to work with here, so let’s use that.
At [latex](1, 6)[/latex] we could choose a number slightly less than 1 to plug into the formula for [latex]f'[/latex] – perhaps use [latex]x = 0[/latex], or [latex]x = 0.9[/latex]. Then we could examine its sign. But we don’t care about the numerical value, all we are interested in is its sign. And for that, we don’t have to do any plugging in:
- If [latex]x[/latex] is a little less than 1, then [latex]x-1[/latex] is negative, and [latex]x-3[/latex] is negative. So [latex]f' = 3(x - 1)(x - 3)[/latex] will be pos(neg)(neg) = positive.
- For [latex]x[/latex] a little more than 1, we can evaluate [latex]f'[/latex] at a number more than 1 (but less than 3, we don’t want to go past the next critical point!) – perhaps [latex]x = 2[/latex]. Or we can make a quick sign argument like what we did above: for [latex]x[/latex] a little more than 1, [latex]f' = 3(x - 1)(x - 3)[/latex] will be pos(pos)(neg) = negative.
So [latex]f'[/latex] changes from positive to negative at [latex]x=1[/latex] and, since [latex]x=1[/latex] is in the domain, there is a local max at [latex](1, 6)[/latex]. We would now repeat the argument for the other critical number, [latex]x=3[/latex].
As another approach, we could create the sign chart for [latex]f'[/latex] by splitting the domain into subintervals using the critical numbers:
| interval test value | [latex]0[/latex] | [latex]2[/latex] | [latex]5[/latex] | ||
| [latex]x[/latex] | [latex](-\infty,1)[/latex] | [latex]1[/latex] | [latex](1,3)[/latex] | [latex]3[/latex] | [latex](3,\infty)[/latex] |
| [latex]f'(x)=3(x - 1)(x - 3)[/latex] | [latex]+--=+[/latex] | [latex]0[/latex] | [latex]++-=+[/latex] | [latex]0[/latex] | [latex]+++=+[/latex] |
| [latex]f(x)[/latex] | increasing | local maximum | decreasing | local minimum | increasing |
This confirms what we saw before in the graph of the function:
Example 5
Determine the local extrema of the following function:
[latex]y=\frac{e^x}{x}[/latex]
Answer: local extrema of [latex]y[/latex]?
Local extrema occur only at critical numbers, so we need to dind the critical numbers of [latex]y[/latex], i.e., the values of [latex]x[/latex] in the domain of [latex]y[/latex] for which [latex]y'[/latex] is undefined or equal to zero.
critical numbers?
critical #s are input values in the domain for which [latex]y'=0[/latex] or undefined [latex]\to[/latex] need the domain,[latex]y'[/latex], and solutions to [latex]y'=0[/latex] or DNE
domain?
domain is all input values that produce an output, i.e., [latex]x=?[/latex] such that [latex]y=\frac{e^x}{x}[/latex] exists
Since [latex]e^x[/latex] is defined for all [latex]x[/latex] and the only other operation is division, which requires that the denominator be non-zero, we have that the only restriction is that [latex]x\neq 0[/latex], i.e.,
domain: [latex](-\infty,0)\cup(0,\infty)[/latex]
[latex]y'=?[/latex]
Since [latex]y[/latex] is a quotient of exp. fn. and linear fn. we have that
[latex]y'=\frac{e^x\cdot x-e^x\cdot 1}{x^2}=\frac{e^x(x-1)}{x^2}[/latex]
[latex]y'=0?[/latex]
Since [latex]y'[/latex] is a quotient, it is equal to zero only when the numerator is zero and the denominator is not zero. Hence
[latex]y'=0\Rightarrow e^x(x-1)=0\Rightarrow e^x=0[/latex] or [latex]x-1=0\Rightarrow x=1[/latex] ([latex]e^x[/latex] is never zero)
Since [latex]x=1[/latex] is in the domain of [latex]y[/latex], [latex]x=1[/latex] is a critical number of [latex]y[/latex].
[latex]y'[/latex] DNE?
Since [latex]y'[/latex] is a quotient of a product of an exponential function with a polynomial, which are defined for all [latex]x[/latex], and the square function (defined for all [latex]x)[/latex]), it is not defined only when its denominator is zero, i.e., when [latex]x^2=0[/latex], i.e., [latex]x=0[/latex], which is not in the domain of [latex]y[/latex] and so it is not a critical number of [latex]y[/latex].
Therefore, [latex]y[/latex] has only one critical number, at [latex]x=1[/latex]. We use this information to create a sign chart for [latex]y'[/latex] by slitting up the domain using the critical number:
| [latex]0[/latex] | [latex]0.5[/latex] | [latex]5[/latex] | |||
| [latex](-\infty,0)[/latex] | [latex]0[/latex] | [latex](0,1)[/latex] | [latex]1[/latex] | [latex](1,\infty)[/latex] | |
| [latex]y'=\frac{e^x(x-1)}{x^2}[/latex] | [latex]\frac{+-}{+}=-[/latex] | [latex]\frac{+-}=-[/latex] | [latex]\frac{++}{+}=+[/latex] | ||
| [latex]f(x)[/latex] | decreasing | not defined | decreasing | local minimum | increasing |
We can verify our findings using a graphing calculator: link to graph
Section Exercises
Work on the following exercises. Discuss your solutions with your peers and/or course instructor.
IC4NITS Exercises 2.8 – First Derivative and the Extrema
