2.6: Implicit Differentiation and Related Rates
2.6: Implicit Differentiation and Related Rates
Implicit Differentiation
In our work up until now, the functions we needed to differentiate were either given explicitly, such as [latex]y=x^2+e^x,[/latex] or it was possible to get an explicit formula for them, such as solving [latex]y^3-3x^2=5[/latex] to get [latex]y=\sqrt[3]{5+3x^2}[/latex]. Sometimes, however, we will have an equation relating [latex]x[/latex] and [latex]y[/latex] which is either difficult or impossible to solve explicitly for [latex]y[/latex], such as [latex]y+e^y=x^2[/latex]. In such cases we can still find [latex]y' = f'(x)[/latex] by using implicit differentiation.
The key idea behind implicit differentiation is to assume that [latex]y[/latex] is a function of [latex]x[/latex] even if we cannot explicitly solve for [latex]y[/latex]. This assumption does not require any work, but we need to be very careful to treat [latex]y[/latex] as a function when we differentiate and to use the Chain Rule.
Video Demonstration
Implicit Differentiation
© 2014 Eric Bancroft
Example 1
Assume that [latex]y[/latex] is a function of [latex]x[/latex]. Calculate
a. [latex]\frac{d}{dx}\left( y^3 \right)[/latex]
b. [latex]\frac{d}{dx}\left( x^3y^2 \right)[/latex]
c. [latex]\frac{d}{dx}\left( \ln(y) \right)[/latex]
Answer:
a. [latex]\frac{d}{dx}\left( y^3 \right)=?[/latex]
Since [latex]y[/latex] is considered to be a function of [latex]x[/latex], we have that
[latex]y^3=\overbrace{({y(x)})^3}^{composition}=\overbrace{(\text{something involving }x)^3}^{composition}[/latex]
Thus we will need the chain rule since [latex]y^3[/latex] is a power function applied to another (unknown) function of [latex]x[/latex], i.e., a composition of functions.
[latex]\frac{d}{dx}\left( y^3 \right)=\overset{out'}{3y^2}\cdot\overset{in'}{\frac{dy}{dx}}\overset{or}{=}3y^2y'[/latex]
b. [latex]\frac{d}{dx}\left( x^3y^2 \right)=?[/latex]
Let's analyze the function:
[latex]x^3y^2=\overbrace{x^3\cdot \overbrace{(y(x))^2}^{composition}}^{product}[/latex]
Therefore we need to use the product rule and the chain rule:
[latex]\begin{align*} \frac{d}{dx}\left( x^3y^2 \right) & = \overset{first'}{3x^2}\cdot \overset{second}{\overset{}{y}}+\overset{first}{\overset{}{x^3}}\cdot\overset{second'}{\underset{out'}{\underset{}{2y}}\cdot\underset{in'}{\underset{}{\frac{dy}{dx}}} }\\ & = 3x^2y+2x^3y\frac{dy}{dx} \\\\ &\overset{\text{or}}{=} 3x^2y+2x^3yy' \end{align*}[/latex]
c. [latex]\frac{d}{dx}\left( \ln(y) \right)=?[/latex]
Since [latex]\ln(y)=\ln(y(x))[/latex], this is a composition of functions with no other operations and so we simply apply the chain rule:
[latex]\frac{d}{dx}\left( \ln(y) \right)=\frac{1}{y}\cdot \frac{dy}{dx}=\frac{1}{y}\cdot y'[/latex]
In the above example we differentiated expressions involving both the input variable and an unknown function of that variable. We will now use this process in determining the derivative of the unknown function if we are given an equation consisting of such expressions. This process is called implicit differentiation. It will involve simultaneously differentiating both sides of the given equation and then rearranging the new equation that now involves the derivative of the unknown function to solve for the derivative
Implicit Differentiation
To determine [latex]y'[/latex], differentiate each side of the defining equation, treating [latex]y[/latex] as a function of [latex]x[/latex], and then algebraically solve for [latex]y'[/latex].
Video Demonstration
Implicit Differentiation - more examples
© 2014 Eric Bancroft
(The last example in the following video gets rather messy - don't worry too much if you can't follow all of the simplifications at the end.)
Video Demonstration
Implicit Differentiation - and more examples
© 2014 Eric Bancroft
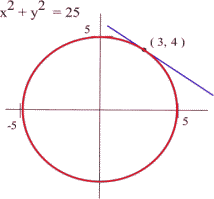
Example 2
Use implicit differentiation to find the slope of the tangent line to the circle [latex]x^2 + y^2 = 25[/latex] at the point [latex](3, 4)[/latex].
Answer: slope of tangent at [latex](3,4)[/latex]?
The slope of the tangent line will be equal to [latex]\frac{dy}{dx}[/latex] evaluated at the point [latex](3, 4)[/latex].
We differentiate each side of the equation [latex]x^2 + y^2 = 25[/latex] with respect to [latex]x[/latex] and then solve for [latex]y'[/latex]:
[latex]\begin{align*} x^2 + y^2 = 25&\Rightarrow \frac{d}{dx}\left(x^2+y^2\right) = \frac{d}{dx}(25)\\\\ &\Rightarrow 2x+2yy' = 0\\\\ &\Rightarrow 2yy'=-2x\\\\ &\Rightarrow y'=-\frac{x}{y} \end{align*}[/latex]
Therefore, at the point [latex](3,4)[/latex], [latex]y'=-\frac{3}{4}[/latex] and so slope of the tangent line at [latex](3, 4)[/latex] is [latex]0.75[/latex].
Example 3
Suppose that the wi-fi signal strength [latex]s[/latex] (measured in dBm) and antenna adjustment [latex]a[/latex] (measured in degrees) are related as follows:
[latex]0.5a^{3}s-2a^{2}s^{2}+0.5=0[/latex]
Determine the rate of change in the signal strength when the antenna is adjusted by 5 degrees, giving the signal strength of 1.258 dBm. Interpret your result.
Answer: [latex]ds/da=?[/latex] when [latex]a=5[/latex] and [latex]s=0.792[/latex]; Interpretation?
The given equation cannot be (easily) solved for [latex]s[/latex], so we will use implicit differentiation.
[latex]\begin{align*} 0.5a^{3}s-2a^{2}s^{2}+0.5=0&\Rightarrow \frac{d}{da}(0.5a^{3}s-2a^{2}s^{2}+0.5)=\frac{d}{da}\left(0\right)\\\\ &\Rightarrow 1.5a^2\cdot s+0.5a^3\cdot\frac{ds}{da}-4as^2-2a^2\cdot \left(2s\cdot \frac{ds}{da}\right)+0=0\\\\ &\Rightarrow 1.5a^2s+0.5a^3\cdot\frac{ds}{da}-4as^2-4a^2s\cdot \frac{ds}{da}=0\\\\ &\Rightarrow \frac{ds}{da}\left(0.5a^3-4a^2s\right)=4as^2-1.5a^2s\\\\ &\Rightarrow \frac{ds}{da}=\frac{4as^2-1.5a^2s}{0.5a^3-4a^2s} \end{align*}[/latex]
At [latex]a=5[/latex] and [latex]s=1.258[/latex] we have
[latex]\dfrac{ds}{da}=\dfrac{4\cdot 5\cdot 1.258^2-1.5\cdot 5^2\cdot 1.258^2}{0.5\cdot 5^3-4\cdot 5^2\cdot 1.258}\approx 0.245[/latex]
and so at 5 degrees in antenna adjustment when the signal strength is 1.258 dBm, the signal strength is increasing by approximately 0.245 dBm per degree in antenna adjustment.
Video Demonstration
Equation of the tangent line using implicit differentiation
© 2014 Eric Bancroft
Related Rates
If several variables or quantities are related to each other and some of the variables are changing at a known rate, then we can use derivatives to determine how rapidly the other variables must be changing.
In particular, suppose we know that there is a relationship between two quantities and that this relationship can be expressed through an equation involving those quantities. Furthermore, suppose both of those quantities are changing in relation to another, third quantity. Then we can use implicit differentiation to determine the rate of change in one of the original two quantities with respect to the third quantity if we know how the second original quantity is changing in relation to the third quantity.
Specifically, we can use the same process we used in the examples above when determining the derivative of [latex]y[/latex] with respect to [latex]x[/latex] given some equation connecting the two, but in this case both of the variables are functions, now of some third variable.
Here is a link to the examples used in the videos in this section: Related Rates.
Video Demonstration
Related Rates - Example 1
© 2014 Eric Bancroft
Example 4
How fast is the surface of a cube increasing if its width is increasing at the rate of 2 cm/min when the width of the cube is 15 cm?
Answer: [latex]\dfrac{dS}{dt}=?[/latex] where [latex]S[/latex] is the surface area (cm2) of a cube and [latex]t[/latex] is time (min), given a width and rate of change in width
Note that we are looking for a rate of change in the surface area and we are given information about the rate of change in width. So we first consider what we know about the relationship between the surface area of the cube and its width. Recalling our knowledge about basic geometry, we know that if [latex]w[/latex] is the width of the cube, then:
[latex]S=6w^2[/latex]
We can now use implicit differentiation to determine the rate of change in the surface area in relation to time by taking the derivative of both sides of that equation with respect to [latex]t[/latex]:
[latex]\begin{align*} S=w^3&\Rightarrow\frac{d}{dt}\left( S \right)= \frac{d}{dt}\left(6w^2 \right)\\ &\Rightarrow\frac{dS}{dt}= 12w\frac{dw}{dt} \end{align*}[/latex]
Substituting in the values we know for [latex]w[/latex] and [latex]\frac{dw}{dt}[/latex], we have
[latex]\frac{dS}{dt}=12(15)(2)=360[/latex]
So the surface area of the cube is increasing by approximately 360 square cm per min when the width is 15 miles and increasing by 2 cm per minute.
Example 5
A company is using an AI-based weekly predictor of the company’s network usage. Its network analysts ran a test that measured the accuracy [latex]A[/latex] of the predictor (as a percent of accuracy) in relation to the number of data points [latex]n[/latex] used by the predictor. They modeled the predictor’s accuracy using
[latex]A(n)=2.55\sqrt{n+250})+40.3[/latex]
If the number of data points is decreasing by 150 per test when the number of data points is 3000, what is the rate of change in the accuracy of the predictor per test? Express your result as a percent, rounded to two decimals. Briefly explain the meaning of your result in the context of the question.
Answer: [latex]\dfrac{dA}{dT}=?[/latex] where [latex]T[/latex] is the number of tests
We are given information about the rate of change in the number of data points in relation to the number of tests and so we can apply implicit differentiation to the relationship between predictor accuracy [latex]A[/latex] and number of data points [latex]n[/latex] to find the rate of change in the accuracy in relation to the number of tests run. In this case we will view both the accuracy and the number of data points as functions of the number of tests (even though the accuracy is also a function of number of data points):
[latex]\begin{align*} A=2.55\sqrt{n+250}+40.3&\Rightarrow A=2.55(n+250)^{1/2}+40.3\\ &\Rightarrow \frac{d}{dT}(A) = \frac{d}{dT}\overset{sum}{\left(\overset{composition}{2.55(n+250)^{1/2}}+\overset{constant}{40.3}\right)} \\ &\Rightarrow \frac{dA}{dT} = 2.55\cdot \frac{1}{2}\left(n+250\right)^{-1/2}\cdot\left(\frac{dn}{dT}+0\right)+0 \\ &\Rightarrow \frac{dA}{dT} = 2.55\cdot \frac{1}{2}\left(n+250\right)^{-1/2}\cdot\frac{dn}{dT} \end{align*}[/latex]
Using the given information, we know the number of data points is decreasing by 150 per test when there are 3000 points, so
[latex]\frac{dA}{dT} = 2.55\cdot \frac{1}{2}\left(3000+250\right)^{-1/2}\cdot(-150)\approx-3.35[/latex]
Therefore, when there are 3000 points and the number of data points is decreasing by 150 per test, the predictor accuracy is decreasing by approximately 3.35% per test.
Section Exercises
Work on the following exercises. Discuss your solutions with your peers and/or course instructor.
IC4NITS Exercises 2.6 - Implicit Differentiation and Related Rates

